DERIVADAS EXPONENCIALES Y LOGARITMICA
Diario de clase# 1
Yedaneira Estrada
En esta clase vimos 3 derivadas más estas igual van relacionadas con las trigonométricas y algebraicas que claro con la práctica se nos van a facilitar más.
Funciones potencial, logarítmica y exponencial
La derivada de una función potencial, que se expresa como f (x) = un (x), se calcula como el producto del exponente por la derivada de la función u (x) y por la función u (x) elevada a un grado menos (n-1).
La derivada de una función logarítmica, de fórmula general f (x) = loga u(x), se obtiene como el cociente de la derivada de u (x) por la propia función u (x) y todo ello multiplicado por el logaritmo en base a del número e. Esta fórmula se simplifica para los logaritmos neperianos, ya que loge e = 1.
Finalmente, para derivar una función exponencial de expresión general f (x) = au(x), se multiplica la propia función por la derivada del exponente, y todo ello multiplicado por el logaritmo neperiano de la base. Como caso particular, hay que resaltar que la función y = ex tiene como derivada ella misma (y ¿= ex).
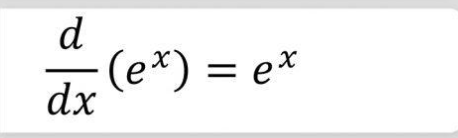
Comentarios
Publicar un comentario