YEDANEIRA ESTRADA

Algebra de conjuntos

Diario #2

21/Oct/2023

En esta clase vimos sobre el diagrama de ven en cómo es su funcionamiento realmente Un diagrama de Ben es un gráfico donde los conjuntos se representan con regiones encerradas en un plano. Aquí el conjunto universo U es el interior de un rectángulo y los otros conjuntos se representan por círculos dentro del rectángulo.

Especificación de conjuntos

Una forma, de ser posible, consiste en enumerar sus elementos separados por comas y escritos entre llaves {}. La segunda es escribir las propiedades que caracterizan a los elementos del conjunto. La recta vertical | se lee “tal que” y la coma “y”.

Diagramas de Benn

Un diagrama de Benn es un gráfico donde los conjuntos se representan con regiones encerradas en un plano. Aquí el conjunto universo U es el interior de un rectángulo y los otros conjuntos se representan por círculos dentro del rectángulo.

Operaciones con Conjuntos

Unión e Intersección

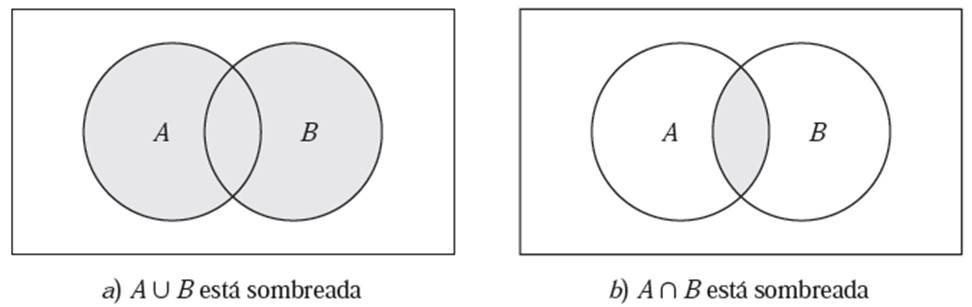
La unión de dos conjuntos A y B, que se denota por A ∪ B, es el conjunto de todos los elementos que pertenecen a A o a B; es decir,

A ∪ B = {x | x ∈ A o x ∈ B}

Expresión Lógica: p ∨ q siendo p: x ∈ A, q: x ∈ B

La intersección de dos conjuntos A y B, que se denota por A ∩ B , es el conjunto de los elementos que pertenecen tanto a A como a B; es decir,

A ∩ B = {x | x ∈ A y x ∈ B}

Expresión Lógica: p ∧ q siendo p: x ∈ A, q: x ∈ B

El álgebra de conjuntos es un área de estudio, dentro de las matemáticas y la lógica, enfocada en las operaciones que pueden efectuarse entre los conjuntos.

El álgebra de conjuntos forma parte de lo que conocemos como teoría de conjuntos.

Cabe recordar que un conjunto es la agrupación de elementos de distinta índole, como pueden ser letras, números, símbolos, funciones, figuras geométricas, entre otros.

Operaciones con conjuntos

Las principales operaciones con conjuntos son las siguientes:

Unión: La unión de dos o más conjuntos contiene todos los elementos que pertenezcan, al menos, a uno de dichos conjuntos. Se indica con la letra U.

A={9,34,57,6,9}

B={10,41,57,9,16}

AUB={9,34,57,6,9,10,41,16}

blank

Intersección: La intersección de dos o más conjuntos incluye los elementos que comparten dichos conjuntos. Se indica con la U invertida(∩). Ejemplo:

A={a,r,t,i,c,o}

B={i,n,d,i,c,o}

A∩B={i,c,o}

Diferencia: La diferencia de un conjunto respecto a otro es a igual a los elementos del primer conjunto menos los elementos del segundo. Se indica con el símbolo \ o con -. Visto de otro modo, x ∈ a A\B si x ∈ A, pero x ∉ B. Ejemplo:

A={21,34,56,17,7}

B={78,21,17,36,80}

A-B={34,56,7}

Complemento: El complemento de un conjunto incluye todos los elementos que no están contenidos en dicho conjunto (pero que sí pertenecen a otro conjunto universal de referencia). Se indica con el superíndice C. Ejemplo:

A={3,9,12,15,18}

U (Universo)=Todos los múltiplos de 3 que sean números naturales enteros menores de 30.

A^C={6,21,24,27}

Diferencia simétrica: La diferencia simétrica de dos conjuntos incluye todos elementos que están en uno o en otro, pero no en ambos al mismo tiempo. Es decir, se trata de la unión de los conjuntos menos su intersección. Su símbolo es Δ. Ejemplo:

A={17,81,99,131,65,32}

B={11,54,71,65,99,27}

AΔB={17,81,131,32,11,54,71,27}