Longitud de arco


21/Oct/23

Diario clase #3                                                                                                             Yedaneira Estrada


                               

Mi aprendizaje de esta clase fue que si se tiene una función F(x) derivable en un intervalo [a, b] entonces podemos medir la longitud de la gráfica en este intervalo. Esta longitud se conoce como longitud del arco de la función F(x).



Ejemplo: Encuentra la longitud de y = x(3/2) de x = 0 a x = 4.

 

La derivada es y’ = (3/2)x(1/2)



Comienza con:

S = 
4
0
 √1+(f’(x))2 dx

Pon (3/2)x(1/2):

S = 
4
0
 √1+((3/2)x(1/2))2 dx

Simplifica:

S = 
4
0
 √1+(9/4)x dx

Podemos usar integración por sustitución:

  • u = 1 + (9/4) x
  • du = (9/4)dx
  • (4/9) du = dx
  • Límites: u(0)=1 y u(4)=10

Y nos queda:

S = 
10
1
 (4/9)√u du

Integra:

S = (8/27) u(3/2) de 1 a 10

Calcula:

S = (8/27) (10(3/2) − 1(3/2)) = 9.073...

Conclusión

La fórmula de longitud de arco para una función f(x) es:

S = 
b
a
 √1+(f’(x))2 dx

Pasos:

  • Calcula la derivada de f(x)
  • Escribe la fórmula de longitud de arco
  • Simplifica y resuelve la integral.














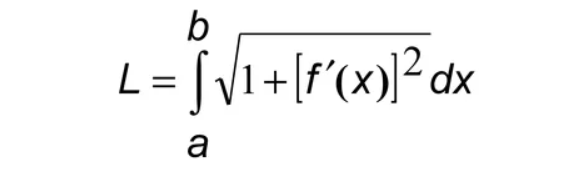
Longitud de Arco (Cálculo) (disfrutalasmatematicas.com)




Comentarios

Publicar un comentario

Entradas más populares de este blog

Imagen
 Resumen de las exposiciones diario #2 11/Nov/23                                              Yedaneira Estrada Las variables aleatorias discretas discretas son aquellos resultados numéricos dados de un experimento Las variables aleatorias discretas son aquellas que toman un conjunto numerable de valores. Por ejemplo, el número de caras obtenidas al lanzar un dado es una variable aleatoria discreta. Ejemplos de variables aleatorias discretas Las variables aleatorias discretas siempre son numéricas y contables. Por lo general miden el número veces que ocurre un suceso, por ejemplo:  *Número de llamadas recibidas por un centro de llamadas en una tarde.  •Cantidad de depósitos bancarios efectuados en un solo día. •Alumnos que aprobaron el examen de Álgebra I, seleccionados al azar de un grupo de 100 estudian ingeniería de una universidad. Valor esperado de una variable aleatoria La esperanza matemática de una variable aleatoria X, es el número que expresa el valor medio del fenómeno que
Leer más
Imagen
 Integración por fracciones parciales Diario #2 11/Nov/23                                                                                                                                                   Yedaneira Estrada Este método permite integrar alguna de las funciones racionales, que difícilmente se puede resolver mediante otros métodos de integración de fracciones parciales es un método algebraico que permite descomponer una fracción racional en la suma de varias funciones. Cómo integrar funciones por fracciones parciales El método de fracciones parciales es usado para integrar funciones racionales de la siguiente forma: Para integrar a una función racional usando fracciones parciales seguimos los siguientes pasos: 1.  Descomponer a la función racional en sus fracciones parciales Puedes hacer una revisión de los métodos de descomposición en fracciones parciales  en este artículo . 2.  Forma una integral con cada fracción parcial La integral de la suma de fracciones es igual a l
Leer más
Imagen
  Cálculo de volúmenes método de discos y arandelas 14/Oct/23 Diario clase 2                                     Yedaneira Estrada Mediante estos métodos he aprendido a calcular los volúmenes sólidos y huecos de las funciones cuando girar sobre el eje X. MÉTODO DE DISCOS El sólido generado al hacer girar una región plana alrededor de un eje se denomina sólido de revolución. Para determinar el volumen de este tipo de sólidos es necesario observar que el área de la sección transversal 𝐴 ( 𝑥 ) es el área de un disco de radio 𝑅 ( 𝑥 ), la distancia de la frontera de la región plana al eje de revolución En este caso la definición de volumen da: MÉTODO DE ARANDELAS O ANILLOS Si la región que gira para generar un sólido no cruza o no hace frontera con el eje de revolución, el sólido tendrá un agujero. Las secciones transversales perpendiculares al eje de revolución son arandelas. Las dimensiones de una arandela representativa son: Radio exterior 𝑹 ( 𝒙 ) Radio interior 𝒓 ( 𝒙 ) El ár
Leer más